Дроби древнего мира
Приглашаем вас в увлекательное путешествие по Древнему миру, в ходе которого мы посетим Египет, Вавилон и Рим.
Будем рады, если размещенная на нашем сайте информация окажется Вам полезной.
muzigipotenuzi.ru

Tilda Publishing
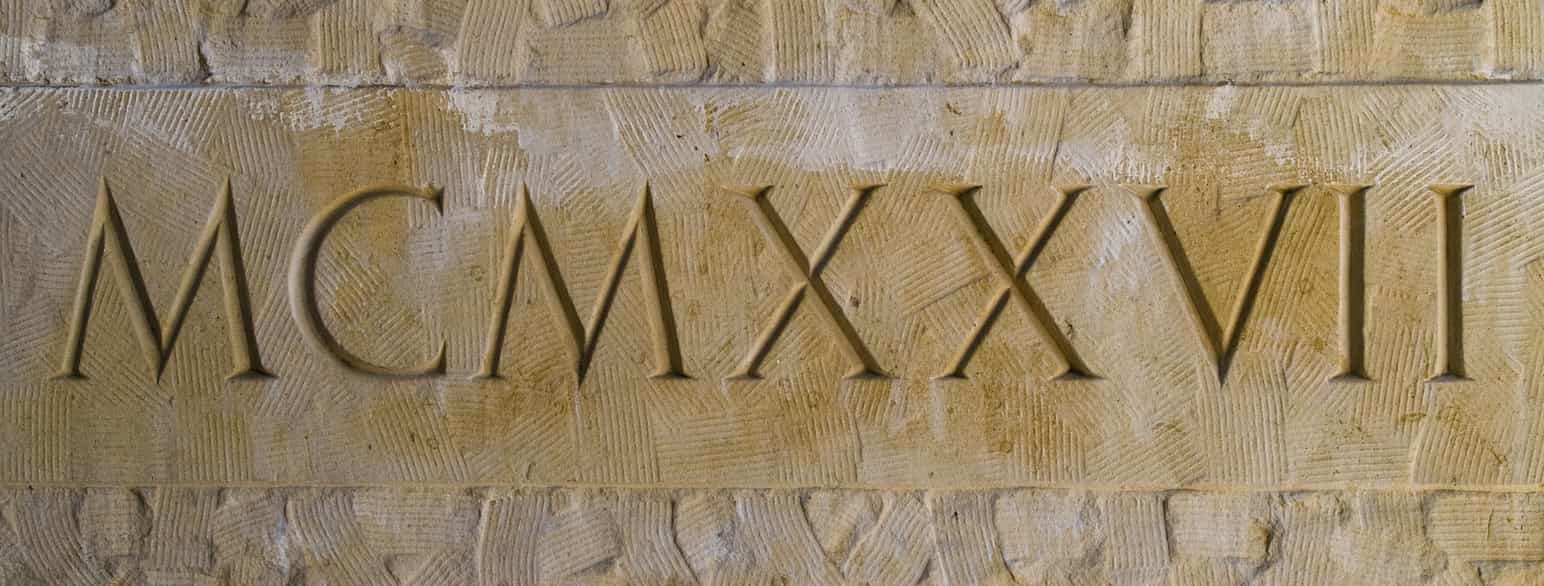

Здесь вы сможете узнать
информацию о системах дробей Древнего мира
информацию о системах дробей Древнего мира
МуZы гипотенуZы
1
Древний Египет
Увы, на сегодняшний день осталось в сохранности мало информации о математике Древнего Египта. Обосновать это можно тем, что папирус, на котором писали египтяне, отличается плохой сохранностью. Однако даже тот объём документов, что смог остаться в целостности до нашего времени, доказывает нам о развитости математики Древнего Египта. Примечательно, учёные Греции и Вавилона перенимали знания у египтян.
Аликвотные дроби
Аликвотной называют дробь с числителем 1, знаменатель которой натуральное число, большее 1.
Аликвотные дроби начали использоваться ещё в древности. Необходимость в дробных числах возникла в результате практической деятельности человека.
Потребность в нахождении долей единицы появилась у наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.
Алгоритм разложения обыкновенных дробей на сумму аликвотных дробей.
Если:
1) Знаменатель - составное число, а значение числителя можно представить в виде суммы делителей знаменателя.
- представить числитель в виде суммы слагаемых, каждое из которых является делителем знаменателя.
- выполнить деление каждого слагаемого числителя на знаменатель (сократить дроби).
- представить числитель в виде суммы слагаемых, каждое из которых является делителем знаменателя.
- выполнить деление каждого слагаемого числителя на знаменатель (сократить дроби).

Если:
2) Знаменатель - составное чилсло, а числитель нельзя представить в виде суммы делителей знаменателя.
ИЛИ
3) Знаменатель – простое число.
ИЛИ
4) Дробь является аликвотной.
- домножить дробь так, чтобы значение числителя стало немного больше значения исходного знаменателя
- представить числитель в виде суммы слагаемых, каждое из которых является делителем для знаменателя (стараясь при этом получить минимальный возможный остаток).
- в случае наличия остатка, не являющегося делителем знаменателя, повторить для последней получившейся дроби все действия алгоритма
ИЛИ
3) Знаменатель – простое число.
ИЛИ
4) Дробь является аликвотной.
- домножить дробь так, чтобы значение числителя стало немного больше значения исходного знаменателя
- представить числитель в виде суммы слагаемых, каждое из которых является делителем для знаменателя (стараясь при этом получить минимальный возможный остаток).
- в случае наличия остатка, не являющегося делителем знаменателя, повторить для последней получившейся дроби все действия алгоритма

Примечание
Существуют специальные формулы, позволяющие выполнить разложение обыкновенных дробей на суммы аликвотных дробей. Мы решили познакомиться с различными вариантами решения и разработали своеобразную инструкцию, которая поможет выбрать оптимальный алгоритм для выполнения задания без формул.
2
Древний Вавилон
Сейчас мы с вами познакомимся с Вавилоном, а точнее с шестидесятеричной системой счисления.
Такое длинное, труднопроизносимое и непонятное название, правда? Давайте разберемся, что это за система такая, откуда она взялась и зачем ее придумали?
Шестидесятеричная система счисления — позиционная система счисления по целочисленному основанию 60.
С одной стороны, шестидесятеричная система удобна тем, что основание системы делится нацело на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30. С другой стороны, наличие 60 цифр создаёт многочисленные неудобства (скажем, таблица умножения насчитывала 1770 строк на глиняных табличках), так что использовавшим эту систему финикийским и вавилонским математикам пришлось разработать специальную технику записи цифр — число изображалось в позиционной 60-ричной системе, а его 60-ричные цифры — в аддитивной десятичной.

Научные гипотезы о возникновении шестидесятиричной системы счисления.
Теон Александрийский (конец 4 - начало 5 века н.э.)
Теон полагал, что число 60 было выбрано вавилонянами за основание системы счисления в силу своих арифметических свойств: оно имеет наибольшее число различных делителей среди сравнительно небольших чисел.
Гипотеза Кевича
(1904)
(1904)
Кевич предполагал, что шестидесятеричная система возникла из смешения двух систем, существовавших прежде независимо: десятеричной и шестеричной. Одна из них, по мнению Кевича, должна быть система исчисления шумеров, другая - аккадян. Гипотеза мало обоснована фактами, оставляла открытым вопрос, какой из двух народов, шумерский или аккадский, имел первоначально шестеричную систему.
Гипотеза Нейгебауера (1927)
Гипотеза О. Нейгебауэра заключается в том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель (сикль) и мина, причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел.
Гипотеза Тюро-Данжена (1932)
Тюро-Данжен предположил, что в древнейшее время вавилонская нумерация имела смешанный десятичный характер; единицей второго разряда служила десятка; единица же третьего разряда образовалась из шести единиц второго разряда, так что роль нашей "сотни" играло число 60. Тюро-Данжен считаел, что причина этого в том, что число 6, делящееся на 2 и 3, оказалось более удобным по своей арифметической структуре.
Гипотеза Веселовского И.Н. (1959)
Гипотеза Веселовского связана с применением двенадцатеричной системы счисления и счёта на пальцах (60 = 5×12, где 5 — число пальцев на руке).
Мы считаем гипотезу Веселовского Н. И. самой правдоподобной, так как:
— счёт с помощью пальцев был самым простым и очевидным для людей, живших более двух тысячелетий назад
— Веселовский Н. И. признавал возникновение шестидесятеричной системы, как комбинации пятеричной и двенадцатеричной систем
— прежде, чем выдвинуть свою гипотезу, он был знаком с предыдущими и имел возможности анализировать их достоинства и недостатки.
Скорее всего, шестидесятеричная система возникла на основе ранее существовавших приёмов исчислений как обобщение опыта использования самых удачных с практической точки зрения систем дробей Древнего Мира.
— счёт с помощью пальцев был самым простым и очевидным для людей, живших более двух тысячелетий назад
— Веселовский Н. И. признавал возникновение шестидесятеричной системы, как комбинации пятеричной и двенадцатеричной систем
— прежде, чем выдвинуть свою гипотезу, он был знаком с предыдущими и имел возможности анализировать их достоинства и недостатки.
Скорее всего, шестидесятеричная система возникла на основе ранее существовавших приёмов исчислений как обобщение опыта использования самых удачных с практической точки зрения систем дробей Древнего Мира.
Вавилонские таблички
Как и во всех древних городах Ближнего Востока, в Вавилоне существовала клинопись - это логосно-слоговое письмо, которое использовалось для написания нескольких языков Древнего Ближнего Востока. Интересно, что в Вавилоне существовали таблички без словесного пояснения. Давайте узнаем, какую функцию выполняли эти таблички и что на них было написано.

Долгое время ученые не могли прийти к единому мнению: для чего же нужны эти таблички. Дело осложнялось тем, что многие из них не дошли до наших дней в целостности, а некоторые и вовсе были утеряны.
Первоначально считалось, что это было пособие для преподавателей математики. С помощью этой «шпаргалки» учителя проверяли, правильно ли дети решали квадратные уравнения
Однако математики Даниэль Мэнсфилд и Норман Уайлдбергер из Университета Нового Южного Уэльса (Австралия) утверждают, что никакого отношения к детским забавам этот артефакт не имеет.
Учёные многих стран мира, исследовав таблички, пришли к единому мнению: глиняные дощечки предназначены для математических расчётов. Но для какой конкретной цели, вот что интересно?!
На данный момент известно, что Вавилонские таблички - самая точная тригонометрическая таблица. Удивительно, но эти кусочки глины абсолютно верно описывают даже теорему Пифагора, хотя были изготовлены за тысячу лет до её открытия.
Безусловно, записи на табличках были призваны осуществлять расчёты, требующиеся в повседневной жизни. Они применялись для вычислений величин площадей участков территорий и зданий, для выполнения расчётов при строительстве жилых домов, храмов, пирамид.
Безусловно, записи на табличках были призваны осуществлять расчёты, требующиеся в повседневной жизни. Они применялись для вычислений величин площадей участков территорий и зданий, для выполнения расчётов при строительстве жилых домов, храмов, пирамид.
На наш взгляд, клинописные математические вавилонские таблички смело можно считать "первым калькулятором", позволяющим получать точные значения, не прибегая к округлению чисел.
3
Древний Рим
Первые достоверные упоминания о римской системе счисления датируются от пятисотых годов до нашей эры
Цифры от 1 до 3 записывались с помощью палочек (I, II, III). Она является простейшей и примитивнейшей нумерацией, в ней был только один знак, который обозначал единицу. Однако тогда было непонятно, как возникли другие символы. На этот счет есть более интересная версия.
Считают, что формат появился благодаря методам пальцевого счета. Так значения от одного до четырех отображались пальцами от указательного до мизинца. Число 5 же (V) – угол между указательным и большим пальцем, а десять соответствует двум рукам, с помощью которых показывается знак X
Римское исчисление является непозиционной системой счисления, в которой для отображения чисел используются буквы латинского алфавита, такие как I, V, X, L, M, C, D.
Римское исчисление является непозиционной системой счисления, в которой для отображения чисел используются буквы латинского алфавита, такие как I, V, X, L, M, C, D.
Система дробей
Древнего Рима
в современном мире.
Римские цифры используются и в наши дни. Мы видим их на циферблатах часов, в нумерации домов или глав печатных изданий. При покупке одежды прекрасно знаем, какой размер нам подойдёт: M или L. Имена царственных персон, даты на памятниках архитектуры, группы химических элементов – содержат, как правило, римские цифры. Да что там говорить, достаточно вспомнить: «Сегодня у нас самостоятельная работа, не забудьте указать номер варианта». И в вашей тетради появляется римская цифра.
В устной речи иногда проскальзывает слово «скрупулёзно» в значении «точно, тщательно, педантично». Скрупул (scrupulum) – единица, используемая в римской системе как 1/288 часть асса, медной монеты. Великобритания, США, Канада, Австралия и ряда других стран до сих пор используют скрупул как меру массы (примерно 1,137 грамма) в фармацевтическом производстве. Моряки знакомы со словами секстант, квадрант. Это названия навигационных приборов для измерения углов при выстраивании траектории курса кораблей. Кроме вышеназванных стран, на Кубе кроме системы мер до сих пор используются римские цифры и в денежной системе.
Таким образом, элементы римской системы дробей дошли и до наших дней.
Таким образом, элементы римской системы дробей дошли и до наших дней.
Подведём итоги нашего виртуального путешествия. Какая же система Древнего мира являлась для своего времени самой развитой?
Мы считаем, вавилонская. Безусловно, система имеет ряд серьёзных недостатков, которых нет в египетской и римской, но преимущества шестидесятеричной «организации дробей» всё же победили. Приведём главные аргументы в пользу выбора нашей команды.
1. Эта система - позиционная. Это свойство обеспечивает единые правила записи чисел и, как следствие, лёгкость выполнения арифметических операций.
2. Обеспечивает высокую точность расчёта значений частных двух чисел без округления.
3. Нашла применение в жизни людей с точки зрения красоты и практичности (столовые приборы, чайно - кофейные сервизы на 6 и 12 персон).
4. Система оказалась самой удобной для отсчёта времени. 12 месяцев в году, в сутках 24 часа, в часе 60 минут, в минуте 60 секунд.
Вавилонская система опередила время. В расшифровке клинописных табличек, в том числе, содержалось доказательство равенства, формулировку которого спустя тысячу (!) лет открыл Пифагор.
2. Обеспечивает высокую точность расчёта значений частных двух чисел без округления.
3. Нашла применение в жизни людей с точки зрения красоты и практичности (столовые приборы, чайно - кофейные сервизы на 6 и 12 персон).
4. Система оказалась самой удобной для отсчёта времени. 12 месяцев в году, в сутках 24 часа, в часе 60 минут, в минуте 60 секунд.
Вавилонская система опередила время. В расшифровке клинописных табличек, в том числе, содержалось доказательство равенства, формулировку которого спустя тысячу (!) лет открыл Пифагор.
Вавилонская система дробей доказала свою актуальность, спустя более двух тысячелетий. Учёные всего мира признают, что вавилонскую систему дробей «придумал гений».
Надеемся, вам понравилась наша небольшая экскурсия по Древнему миру. Будем рады новой встрече!
